学习一下古典密码学。

古典密码学

1
2
3
4
5
6
密码(Cryptology)是一种用来混淆的技术,它希望将正常的、可识别的信息转变为无法识别的信息。
密码学(Cryptography),是一门将信息进行加密处理与传递,以及分析加密信息的学科。

密码学的发展大概经历了三个阶段:古典密码阶段、近代密码阶段、现代密码阶段。
一般来说，古典密码学是基于字符的，而现代密码学是基于二进制位的。
古典密码阶段是指从密码的产生到发展成为近代密码之间的这段时期密码的发展历史。

古典密码编码方法归根结底主要有两种，即置换和代换。

  • 把明文中的字母重新排列，字母本身不变，但其位置改变了，这样编成的密码称为置换密码。最简单的置换密码是把明文中的字母顺序倒过来，然后截成固定长度的字母组作为密文。

  • 代换密码则是将明文中的字符替代成其他字符。

置换密码

置换密码（permutation cipher）又称为换位密码（transposition cipher），是根据一定的规则重新排列明文，以便打破明文的结构特性。置换密码的特点是保持明文的所有字符不变 ，只是利用置换打乱了明文字符的位置和次序 。也就是说，改变了明文的结构，不改变明文的内容。这种密码是把明文中各字符的位置次序重新排列来得到密文的一种密码体制。

举例，我们来看一种简单的置换密码字母移位

1
2
3
4
5
6
crypto='abc'
for i in range(len(crypto)):
    print(crypto[i:]+crypto[:i])
#abc
#bca
#cab

可以看到我们将每个单词中的字母都向右移动了一位，我们并没有改变明文的内容，只是改变了明文的结构。

最常见的置换密码有：

1
2
3
4
周期置换密码：将明文P按固定长度m分组然后对每组按1，2…，m的某个置换重排位置从而得到密文C
列置换密码：明文P遵照密钥的规程按列换位并且按列读出序列得到密文C
曲路密码：明文P填入一个表中，并按照一定的曲路遍历
栅栏密码：把文本按照一定的字数分成多个组，取每组第一个字连起来得到密文1，再取每组第二个字连起来得到密文2……最后把密文1、密文2……连成整段密文。

周期置换密码

周期置换密码是将明文字符串P按固定的长度m进行分组，然后对每组字符串中的字符按照某个密钥重新排位的到密文C。其中密钥S包含分组长度信息。

1
2
3
4
5
6
7
8
明文：P=flag{012345}
加密的密钥：S=(1 5 6 2 3)
将明文分为两组，每组6个字符，不足6个的用规定好的字符进行填充，比如空格。
现在分组情况是 P'=flag{0+12345}
对每组的字符进行加密，根据密钥S，可知将第1个字符放在第5个字符的位置，第5个字符放在第6个字符的位置，第6个字符放在第2个字符的位置，第2个字符放在第3个字符的位置，第3个字符放在第1个字符的位置,置换后P'如下：
flag{0	------>	a0lgf{
12345}	------>	3}2415
所以得到的最终密文Pm=a0lgf{3}2415

解密时只需得到密钥S的逆置换，把密文重新分组，按照密钥的逆置换对密文的子字符串重新排位就可以得到明文P。

1
2
3
4
5
6
7
密文：P=a0lgf{3}2415
加密的密钥：S=(1 5 6 2 3)
加密的密钥逆置换S` = (1 3 2 6 5)
对每组的字符进行加密，根据密钥逆置换，可知将第1个字符放在第3个字符的位置，第3个字符放在第2个字符的位置，第2个字符放在第6个字符的位置，第6个字符放在第5个字符的位置，第5个字符放在第1个字符的位置,置换后P'如下：
a0lgf{	------>	flag{0
3}2415	------>	12345}
所以得到最后的原文flag{012345}

列置换密码

将明文p以设定的固定分组宽度m按行写出，即每行有m个字符；若明文长度不是m的整数倍，则不足部分用双方约定的方式填充（如双方约定用空格代替空缺处字符），最后得字符矩阵[Mp]n×m，按1，2…，m的某一置换σ交换列的位置次序得字符矩阵[Mp]n×m，把矩阵按[Mp]n×m列的顺序依次读出得密文序列c。

1
2
3
4
5
6
7
8
9
10
明文：P=flag{012345}
分组宽为m=4,得3行4列矩阵M:
M= [f   l   a   g
	{	0	1	2
	3	4	5	}]
置换σ=(1 3)(2	4)#也就是将第1列跟第3列做位置交换，第2列跟第4列做位置交换
M'=[a   g   f   1
	1	2	{	0
	5	}	3	4]
得到密文信息a15g2}f{3104

将密文c以分组宽度n按列写出得到字符矩阵[Mp]n×m，按加密过程用的置换σ的逆置换σ-1交换列的位置次序得字符矩阵[Mp]n×m，把矩阵[Mp]n×m按1，2…，n行的顺序依次读出得明文p

1
2
3
4
5
6
7
8
9
先把密文信息a15g2}f{3104转换成3行4列矩阵M(置换规则是4个数字)
M'=[a   g   f   1
	1	2	{	0
	5	}	3	4]
加密的置换算法逆置换σ=(3 1)(4 2)#也就是将第3列跟第1列做位置交换，第4列跟第2列做位置交换
M= [f   l   a   g
	{	0	1	2
	3	4	5	}]
得到最后的原文flag{012345}
  • 列置换的另一种说法

首先能够把明文去掉空格后，分成分成n×m的一个矩阵如果有空格可以使用约定的字符进行加密，然后根据密钥的顺序依次读取数据。

1
2
3
4
5
6
7
8
9
明文：P=flag{012345}
分组宽为m=4,得3行4列矩阵M:
置换规则σ=(3	1	4	2)	#有的给定一个单词用单词在字母表中的顺序确定置换规则cadb
	3	1	4	2	#对应到矩阵列上面
M= [f   l   a   g
	{	0	1	2
	3	4	5	}]
根据置换规则的序号依次拼接完整信息得到完整的密文信息
得到密文信息l04g2}f{3a15

解密过程就是根据原来的置换规则的逆规则

1
2
3
4
5
6
7
8
9
10
现有密文信息l04g2}f{3a15
置换规则是4个数字所以生成一个4列*3行的矩阵
置换规则σ=(3	1	4	2)的逆向规则σ'=(2	4	1	3)
先分组l04+g2}+f{3+a15，生成矩阵
	2	4	1	3	#对应到矩阵列上面
M= [l   g   f   a
	0	2	{	1
	4	}	3	5]
根据置换规则的序号依次拼接完整信息得到完整的密文信息
得到密文信息flag{012345}

hint：列置换密码算法需要知道密钥的长度和顺序

曲路密码

将明文p以设定的固定分组宽度m按行写出，即每行有m个字符；若明文长度不是m的整数倍，则不足部分用双方约定的方式填充（如双方约定用空格代替空缺处字符），最后得字符矩阵[Mp]n×m，按照一定顺序从头到位遍历所有的字符，把读取到的字符拼接得到密文。

1
2
3
4
5
6
7
8
9
10
11
12
13
加密的文本flag{012345},长度为12
可以使用2*6、3*4的矩阵填入全部的字符，这边选3*4也就是3行×4列
首先将加密的文本按行填入该矩阵,如下面所示
	f   l   a   g
    {	0	1	2
	3	4	5	}
此时按照约定的顺序遍历所有的字符
		<-------		<-------
	f	|	l   ^	a	|	g	^
    {	|	0	|	1	|	2	|
	3	↓	4	|	5	↓	}	|
	(结束)	   <-------		 (开始)
按照次顺序以此取出矩阵中的元素即得到密文信息：}2ga1540lf{3

给定加密密码和矩阵规格，也容易得到原文，需要事先双方约定密钥（即曲路路径）

只需要按照同样的顺序首先把加密码填入矩阵，然后按照行顺序取出组合在一起

1
2
3
4
5
6
7
8
9
现有密文：}2ga1540lf{3，长度为12
原文密码的矩阵是3*4也就是3行×4列
所以第一个字符就是最左下角，逆向读取每个字符得到原文
		<--------		<--------
	*	|	*   ^	*	|	*	↑
    {	|	*	|	*	|	2	|
	3	↓	*	|	*	↓	}	|
	(开始)	   <-------		 (开始)
也可以画一个表格然后每个字符填入即可得到原文：flag{012345}

栅栏密码

栅栏密码（Rail-fence Cipher）就是把要加密的明文分成N个一组，然后把每组的第1个字符组合，每组第2个字符组合…每组的第N个字符组合，最后一个分组需要满足N个不满足的话就用一个填充符号，最后把他们全部连接起来就是密文（分成几组要求是根据明文长度来，因数关系）

1
2
3
4
5
6
7
8
9
10
明文：P=flag{012345}，明文长度是12可以分成2，3，4，6个一组
加密的密钥：N=2，3，4，6
按照每6个字符组成一组，分成两组，
现在分组情况是第一组flag{0、第二组12345}
分别取每组的第一个字符组成密文1，再取每组第二个字连起来得到密文2...
然后全部密文拼接得到后来的密文
flag{0	+	12345}
第一组f1、第二组l2、第三组a3、第四组g4、第五组{5、第六组0}
f1l2a3g4{50}
所以得到的最终密文f1l2a3g4{50}，称为6栏加密

python脚本实现栅栏密码加密过程

1
2
3
4
5
6
N=栏数
crypto=明文
for i in range(0,N):
    for n in range(i,len(crypto),N):
        print(crypto[n],end='')
#外层循环用于分组，内循环用步长取值，判断一下取值就大概了解原理了
  • 明文或密文中如果出现连续空格将原样保留。
  • 在进行多行文本\段落加密时，每行独立进行加密。
  • N的取值范围在2到明文长度-1之间。

python脚本实现栅栏密码解密过程

1
2
3
4
5
zhalan='f1l2a3g4{50}'
for i in range(0,2):
    for n in range(i,len(zhalan),2):
        flag=flag+zhalan[n]
        print(zhalan[n], end='')

hint：现有明文长度是a=b*c，当明文经过b栏加密后，将密文再次通过c栏加密可以恢复明文

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 栅栏加解密合并
def railfence(content):
    all=[]
    for key in range(2,len(content)):
        flag=''
        if len(content)%key==0:
            for i in range(0, key):
                for n in range(i, len(content), key):
                    flag=flag+content[n]
                    # print(content[n], end='')
            all.append('栏数为:{0}时,结果为:{1}'.format(key,flag))
    print(all)
    print(len(all))
if __name__ == '__main__':
    content='flag{012345}'
    railfence(content)
    content='f{3l04a15g2}'
    railfence(content)

代换密码

又称为替换密码就是将明文中的每个字母由其它字母、数字或符号替代的一种方法。代换密码通常要建立一个替换表，加密时将需要加密的明文依次通过查表，替换为相应的字符，明文字符被逐个替换后，生成无任何意义的字符串，即密文，这些替换表就作为密钥。代换密码中，则可以认为是保持明文的符号顺序，但是将他们用其他符号来替代。

  • 单表替换密码

又称为单字母替换，明文字母表中的一个字符对应密文字母表中的一个字符。即对明文消息中出现的同一个字母，在加密时都使用同一固定的字母来代换。

  • 多表替换密码

指两个以上替换表依次对明文消息的字母进行替换。明文消息中出现的同一个字母，在加密时不是完全被同一固定的字母代换，而是根据其出现的位置次序，用不同的字母代换。例如，使用有5个替换表的替换密码，明文的第一个字母对应第一个替换表，第二个字母对应第二个替换表,以此类推。

单表替换密码

在单表替换加密中，所有的加密方式几乎都有一个共性，那就是明密文一一对应。所以说，一般有以下两种方式来进行破解

  • 在密钥空间较小的情况下，采用暴力破解方式
  • 在密文长度足够长的时候，使用词频分析

当密钥空间足够大，而密文长度足够短的情况下，破解较为困难。

摩斯电码

摩尔斯电码（又译为摩斯电码，Morse code）是一种时通时断的信号代码，这种信号代码通过不同的排列顺序来表达不同的英文字母、数字和标点符号等。它发明于1837年，发明者有争议，是美国人塞缪尔·莫尔斯或者艾尔菲德·维尔。

摩尔斯电码的符号由两种基本信号和不同的间隔时间组成：短促的点信号“ .”，保持一定时间的长信号“-”。

可以借助在线工具对信息做加解密

1
2
3
4
5
hello world
加密得到
···· · ·－·· ·－·· －－－   ·－－ －－－ ·－· ·－·· －·· 
解密得到
hello world

python实现莫斯解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#莫斯密码加解密
def mosdecrypt(content):
    MorseList = {'A': ".-", 'B': "-...", 'C': "-.-.", 'D': "-..", 'E': ".", 'F': "..-.", 'G': "--.",
                 'H': "....", 'I': "..", 'J': ".---", 'K': "-.-", 'L': ".-..", 'M': "--", 'N': "-.",
                 'O': "---", 'P': ".--.", 'Q': "--.-", 'R': ".-.", 'S': "...", 'T': "-", 'U': "..-",
                 'V': "...-", 'W': ".--", 'X': "-..-", 'Y': "-.--", 'Z': "--..",
                 '1': ".----", '2': "..---", '3': "...--", '4': "....-", '5': ".....",
                 '6': "-....", '7': "--...", '8': "---..", '9': "----.", '0': "-----",
                 '.': ".-.-.-", '?': "..--..", '!': "-.-.--", '(': "-.--.", '@': ".--.-.", ':': "---...",
                 '=': "-...-", '-': "-....-", ')': "-.--.-", ',': "--..--", '\'': ".----.", '_': "..--.-",
                 '$': "...-..-", ';': "-.-.-.", '/': "-..-.", '\"': ".-..-.", '&': ".-...",
                 '+': ".-.-.",
                 'à': ".--.-", 'ä': ".-.-", 'ch': "----", 'ç': "-.-..", 'ð': "..--.",
                 'é': "..-..", 'è': ".-..-", 'ĝ': "--.-.", 'ĥ': "-.--.", 'ĵ': ".---.",
                 'ñ': "--.--", 'ø': "---.", 'ŝ': "...-.", 'þ': ".--..", 'ü': "..--",}
    if '0' in content and '1' in content:
        trans = ''.maketrans('01', '.-')
        content = content.translate(trans)
    if '－' in content or '·' in content:
        content=content.replace('－','-')
        content=content.replace('·','.')
    if '/' in content:
        lmorsecodeList = content.split("/")
    else:
        content = content.replace(' ', '/')
        if '///' in  content:
            content = content.replace('///', '/ /')
        lmorsecodeList = content.split("/")
    print(lmorsecodeList)
    flag = ''
    for char in lmorsecodeList:
        if char ==' ':
            flag = flag +  char
        for k, v in MorseList.items():
            if v == char:
                flag = flag + k
    print("莫斯密码小写:", flag)
    print("莫斯密码大写:", flag.lower())
    return flag
content='··   ·－·· －－－ ···－ ·   －·－－ －－－ ··－ '
print(mosdecrypt(content))
#莫斯密码目前感觉最全的：https://mosimima.wncx.cn/脚本中只对01做了转换

hint：摩斯电码默认采用空格分隔，现在许多摩斯电码采用单斜杠/进行分隔

部分摩斯电码在线网站存在无法解密特殊字符的现象，需要仔细辨别（若干次被坑）

还有一种变体摩斯电码给的里面的信息只有两种字符组成并且能够跟摩斯电码高度相似，比如滴答之类的

凯撒密码

在密码学中，凯撒密码（英语：Caesar cipher），或称凯撒加密、凯撒变换、变换加密，是一种最简单且最广为人知的加密技术。它是一种替换加密的技术，明文中的所有字母都在字母表上向后（或向前）按照一个固定数目进行偏移后被替换成密文。例如，当偏移量是3的时候，所有的字母A将被替换成D，B变成E，以此类推。这个加密方法是以罗马共和时期凯撒的名字命名的，当年凯撒曾用此方法与其将军们进行联系。

  • 加密原理

明文信息X=20，密文信息Y=0，密钥K=3

加密公式：(X+K) mod 26 (python取模符号是%) (20+3)%26=23

解密公式：(Y-K) mod 26 (python取模符号是%) (0-3)%26=(-3+26)%26=23

hint：28%26=2（模的结果不会比26还大，此时的结果能够在0到25之间）

1
2
3
4
5
6
7
8
9
10
11
12
13
content='WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ'
n=3
#-97或者-65是为了保证值在0到25之间
print(''.join([chr(65+(ord(i)+n-65)%26) for i in  content]))#推导式的形式
#ZNKWWAOIQWHXUCTWLUDWPASVYWUBKXWZNKWRGFEWJUM
print(''.join([chr(97+(ord(i)+n-97)%26) for i in  content]))
#theqquickqbrownqfoxqjumpsqoverqtheqlazyqdog
mi=''
for i in content:
    print(ord(i) + n - 97, i)
    mi = mi + chr(97 + (ord(i) + n - 97) % 26)  # -97是为了保证值在0到25之间
print(mi)
#theqquickqbrownqfoxqjumpsqoverqtheqlazyqdog
  • 注意事项

（1）需要区分字母的大小写

（2）如果不是大小写字母，那么就原样输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#凯撒密码
def caesar_Crypto(content):
    all_plain=[]
    for num in range(1,26):
        plain = ''
        for i in content:
            if i.islower():#小写字母
                plain = plain + chr(97 + (ord(i) + num - 97) % 26)
            elif i.isupper():#大写字母
                plain = plain + chr(65 + (ord(i) + num - 65) % 26)
            else:#上面两者都不是
                plain=plain+i
        print(plain)
        all_plain.append(plain)
    print(all_plain)
content='IODJ{Khuh_lv_brxu_iodj}'
caesar_Crypto(content)

还有一种新的思路：

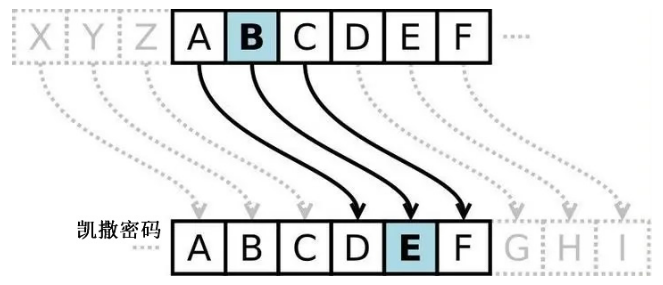
可以看到凯撒的原文跟密文是一对一的，所以可以灵活利用替换的思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# # 凯撒密码
def caesar_Crypto(content):
    all_plain=[]
    lowercase = 'abcdefghijklmnopqrstuvwxyz'
    uppercase = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
    for num in range(1,26):
        lower=lowercase[num:]+lowercase[:num]
        upper=uppercase[num:]+uppercase[:num]
        plain=''
        table=''.maketrans(lower+upper,lowercase+uppercase)
        for i in content:
            plain=plain+i.translate(table)
        all_plain.append(plain)
        print(plain)
    print(all_plain)
content='IODJ{Khuh_lv_brxu_iodj}'
caesar_Crypto(content)
  • 变异凯撒
1
2
加密密文：afZ_r9VYfScOeO_UL^RWUc
格式：flag{ }
1
2
3
4
print(ord(str[0]),ord('f'),ord('f')-ord(str[0]))	97 	102 5
print(ord(str[1]),ord('l'),ord('l')-ord(str[1]))	102 108 6
print(ord(str[2]),ord('a'),ord('a')-ord(str[2]))	90 	97 	7
print(ord(str[3]),ord('g'),ord('g')-ord(str[3]))	95 	103 8

通过acsii码值对比表可以看到第一个字符向后移了5，第二个向后移了6，第三个向后移了7，以此类推

变异凯撒即每个向后移的位数是前一个加1

1
2
3
4
5
6
str="afZ_r9VYfScOeO_UL^RWUc"
num=5
for i in str:
    print(chr(ord(i)+num),end='')
    num=num+1
#flag{Caesar_variation}

rot族解密

编码是一种简单的码元位置顺序替换暗码。此类编码具有可逆性，可以自我解密，主要用于应对快速浏览，或者是机器的读取，而不让其理解其意。ROT5 是 rotate by 5 places 的简写，意思是旋转5个位置，其它皆同。

rot5

只对数字进行编码，用当前数字往前数的第5个数字替换当前数字，例如当前为0，编码后变成5，当前为1，编码后变成6，以此类推顺序循环。

1
2
0123456789
5678901234
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#ROT5
def caesar_Crypto(content):
    all_plain=[]
    lowercase = '0123456789'		 #此处需要修改
    lower=lowercase[5:]+lowercase[:5]#此处需要修改
    plain=''
    table=''.maketrans(lower,lowercase)
    for i in content:
        plain=plain+i.translate(table)
    all_plain.append(plain)
    print(plain)
content='flag{5678901}'
caesar_Crypto(content)
#flag{0123456}
rot13

只对字母进行编码，用当前字母往前数的第13个字母替换当前字母，例如当前为A，编码后变成N，当前为B，编码后变成O，以此类推顺序循环。

1
2
3
4
5
abcdefghijklmnopqrstuvwxyz			明码表
nopqrstuvwxyzabcdefghijklm			密码表
或者
ABCDEFGHIJKLMNOPQRSTUVWXYZ			明码表
NOPQRSTUVWXYZABCDEFGHIJKLM			密码表

hint：rot13就是位移量为13的凯撒密码

rot18

这是一个异类，本来没有，它是将ROT5和ROT13组合在一起，为了好称呼，将其命名为ROT18。

1
2
3
4
5
abcdefghijklmnopqrstuvwxyz0123456789		明码表
nopqrstuvwxyzabcdefghijklm5678901234		密码表
或者
ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789		明码表
NOPQRSTUVWXYZABCDEFGHIJKLM5678901234		密码表
rot47

对数字、字母、常用符号进行编码，按照它们的ASCII值进行位置替换，用当前字符ASCII值往前数的第47位对应字符替换当前字符，例如当前为小写字母z，编码后变成大写字母K，当前为数字0，编码后变成符号_。用于ROT47编码的字符其ASCII值范围是33－126，位移量为47。用于ROT47编码的字符其ASCII值范围是33－126（原因是由于0-32以及127与字符表示无关！！）

1
2
!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~	明码表
PQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNO	密码表

简单替换密码

Atbash Cipher

埃特巴什码（Atbash Cipher）其实可以视为下面要介绍的简单替换密码的特例，它使用字母表中的最后一个字母代表第一个字母，倒数第二个字母代表第二个字母。在罗马字母表中，它是这样出现的：

1
2
ABCDEFGHIJKLMNOPQRSTUVWXYZ		明码表
ZYXWVUTSRQPONMLKJIHGFEDCBA		密码表

比如

1
2
明文：the quick brown fox jumps over the lazy dog
密文：gsv jfrxp yildm ulc qfnkh levi gsv ozab wlt

这种可以使用python实现或者在线网站做词频分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Atbash Cipher
def caesar_Crypto(content):
    all_plain=[]
    lowercase = 'abcdefghijklmnopqrstuvwxyz'
    lower=lowercase[::-1]#此处需要修改
    plain=''
    table=''.maketrans(lower,lowercase)
    for i in content:
        plain=plain+i.translate(table)
    all_plain.append(plain)
    print(plain)
content='the quick brown fox jumps over the lazy dog'
caesar_Crypto(content)			#加密
content='gsv jfrxp yildm ulc qfnkh levi gsv ozab wlt'
caesar_Crypto(content)			#解密
词频分析

凯撒密码的密钥空间只有25所以导致凯撒被破解的可能性就很大了，于是在凯撒密码的基础上出现了简单替换密码（Simple Substitution Cipher）加密时，将每个明文字母替换为与之唯一对应且不同的字母。它与凯撒密码之间的区别是其密码字母表的字母不是简单的移位，而是完全是混乱的，这也使得其破解难度要高于凯撒密码。 比如：

1
2
ABCDEFGHIJKLMNOPQRSTUVWXYZ		明码表
RSTUVWXYZLMNOPQEFGHIJKCDBA		密码表

这种在解密时，我们一般是知道了每一个字母的对应规则，才可以正常解密。

由于这种加密方式导致其所有的密钥个数是26!(26阶乘) ，所以几乎上不可能使用暴力的解决方式

所以我们 一般采用词频分析在线网站：http://quipqiup.com/

培根密码

培根密码，又名倍康尼密码（英语：Bacon’s cipher）是由法兰西斯·培根发明的一种隐写术。密文只有两个a和b，每个明文对应的字符都对应一个有a或b组成的长度是五的字符串。

加密时，明文中的每个字母都会转换成一组五个英文字母。其转换依靠下表：

明文 密文 明文 密文 明文 密文 明文 密文
A/a aaaaa H/h aabbb O/o abbba V/v babab
B/b aaaab I/i abaaa P/p abbbb W/w babba
C/c aaaba J/j abaab Q/q baaaa X/x babbb
D/d aaabb K/k ababa R/r baaab Y/y bbaaa
E/e aabaa L/l ababb S/s baaba Z/z bbaab
F/f aabab M/m abbaa T/t baabb
G/g aabba N/n abbab U/u babaa

密码表二：

明文 密文 明文 密文 明文 密文 明文 密文
A/a aaaaa G/g aabba N/n abbaa T/t baaba
B/b aaaab H/h aabbb O/o abbab UV/uv baabb
C/c aaaba IJ/ij abaaa P/p abbba W/w babaa
D/d aaabb K/k abaab Q/q abbbb X/x babab
E/e aabaa L/l ababa R/r baaaa Y/y babba
F/f aabab M/m ababb S/s baaab Z/z babbb 
1
需要注意的是：i-j ABAAA和u-v BAABB有可能存在不一样的语义，需要结合上下文

加密者需使用两种不同字体，分别代表A和B。按照密文格式化假信息，即依密文中每个字母是A还是B分别套用两种字体。
解密时，将上述方法倒转。所有字体一转回A，字体二转回B，以后再按上表拼回字母。

密文：To encodeamessage each letteroftheplaintextis replaced by a group of fiveofthe letters’A’or ‘B’.

明文：BAABA BAABB AABAA AABBA AAAAA ABBAB ABBBA AABBA BAAAB AAAAA ABBBB AABBB BBAAA

    s   t   e   g   a   n   o   g   r   a   p   h   y

另外一种方法，其将大小写分别看作A与B，可用于无法使用不同字体的场合（例如只能处理纯文本时）。但这样比起字体不同更容易被看出来，而且和语言对大小写的要求也不太兼容。
培根密码本质上是将二进制信息通过样式的区别，加在了正常书写之上。

密文：SjkLnIljKHamJmkilABawiiioaAMbOaPIJmklNBaKijmBuaoljiAUWMakMHWNAakm

明文：BAABA BAABB AABAA AABBA AAAAA ABBAB ABBBA AABBA BAAAB AAAAA ABBBB AABBB BBAAA

    s   t   e   g   a   n   o   g   r   a   p   h   y

python实现培根密码表一的解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
txt='SjkLnIljKHamJmkilABawiiioaAMbOaPIJmklNBaKijmBuaoljiAUWMakMHWNAakm'
content=''
for i in txt:
    if i.islower():
        content+='a'
    elif i.isupper():
        content+="b"
if len(content)%5==0:
    # alphabet = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
    alphabet=[chr(i) for i in range(ord('a'),ord('z')+1)]
    cipher = ["aaaaa","aaaab","aaaba","aaabb","aabaa","aabab","aabba","aabbb","abaaa","abaab","ababa","ababb","abbaa","abbab","abbba","abbbb","baaaa","baaab","baaba","baabb","babaa","babab","babba","babbb","bbaaa","bbaab"]
    key =dict(zip(cipher,alphabet))#生成键值对应的字典
    try:
        flag = ''
        for i in range(0,len(content),5):
            value=content[i:i+5]#切片
            flag+= key.get(value)#取键值
    except:
        flag = ''
        table=''.maketrans("ab","ba")#考虑到不知道ab对应的关系做一次转换
        content=content.translate(table)
        for i in range(0, len(content), 5):
            value = content[i:i + 5]#切片
            flag += key.get(value)#取键值
    print(flag)
else:
    print("不是培根密码")

python实现培根密码表二的解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
content='ABABAABAAABAABBAABAA'.lower()
if len(content) % 5 == 0:
    alphabet = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', '(ij)', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't','(uv)', 'w', 'x', 'y', 'z']
    cipher = ["aaaaa", "aaaab", "aaaba", "aaabb", "aabaa", "aabab", "aabba", "aabbb", "abaaa", "abaab",
              "ababa", "ababb", "abbaa", "abbab", "abbba", "abbbb", "baaaa", "baaab", "baaba", "baabb",
              "babaa", "babab", "babba", "babbb"]
    key = dict(zip(cipher, alphabet))  # 生成键值对应的字典
    try:
        flag = ''
        for i in range(0, len(content), 5):
            value = content[i:i + 5]  # 切片
            flag += key.get(value)  # 取键值
    except:
        flag = ''
        table = ''.maketrans("ab", "ba")
        content = content.translate(table)
        for i in range(0, len(content), 5):
            value = content[i:i + 5]  # 切片
            flag += key.get(value)  # 取键值
    print(flag)
else:
    print("不是培根密码")

还有一种不太常用的方法

密文：xgdocpdcuuhlpfmglupfdlbhekpxiqknvpiimyykoeahrjjcfkmqusrkbuutqvlfb

明文：BAABA BAABB AABAA AABBA AAAAA ABBAB ABBBA AABBA BAAAB AAAAA ABBBB AABBB BBAAA     

​ s   t   e   g   a   n   o   g   r   a   p   h   y

1
2
a--m  --> A:	字母a到m这一范围内的字母统一换成A 
n--z  --> B:    字母n到z这一范围内的字母统一换成B

培根密码所包含的信息可以和用于承载其的文章完全无关。

在线工具：http://rumkin.com/tools/cipher/baconian.php

仿射密码

仿射密码为单表替换密码的一种，字母系统中所有字母都藉一简单数学方程加密，对应至数值，或转回字母。

凯撒密码是将明文与密钥相加得到密文，仿射密码则是将明文与密钥的一部分相乘然后加上密钥的另一部分得到

为了方便计算将26个字母分别用数字表示：a=0，b=1，… ，z=25。

仿射加密的密钥有两个a和b，取值范围都是0到25之间。主要对a有要求，b没有要求：

  • a要求与26互质（互质就是这两个数的公因数只有1）hint：这样的话
    • 26的因数有：1，2，13
    • 上述的结果要求a的因数不包含2或者13即可

仿射密码加密：假设x是明文，y是密文，加密公式y=(a×x+b)mod26，密文=（明文×乘数+位移数）mod 26(mod取值就在0到25之间)

具体过程可以代入数字表示，当a=7，b=3时，加密公式变成了：密文=（明文×7+3）mod 26

当明文等于c的时候：（明文×7+3）mod 26=（2×7+3）mod 26=17=y也就是r密文

解密明文=（密文-b）/a结果有可能是小数无法做mod运算，于是可以使用除法变成乘法，（密文-b）/a转换为（密文-b）a的乘法逆元

所以问题变成了怎么去找到这个a的乘法逆元

  • 乘法逆元

假设用m表示a的乘法逆元，那么(a*m)mod 26=1

当a=7可以用代码实现求m，并且我们只需要一个符合条件的即可

1
2
3
4
5
6
7
8
9
10
11
m=1
while True:
    if (7*m)%26==1:
        print(m)
        break
    m=m+1
#15
for i in range(0,26):
    if (7 * i) % 26 == 1:
        print(i)
#15

所以a的乘法逆元就是15，然后代入公式x=15（17-m）mod26=（15×14）mod26=2所以得到明文是c

1
2
3
4
5
6
7
8
9
10
11
12
#加密公式：c=(11m+7)mod26,对应的a=11,b等于7		密文信息：dikxourxd

content = 'dikxourxd'
m = 1
while True:
    if (11 * m) % 26 == 1:
        print(m)  # 得到乘法逆元
        break
    m = m + 1
for i in content:
    print(chr(97 + (ord(i) - 97 - 7) * 19 % 26))
#ctfsdnisc
  • 暴力破解
1
2
3
4
5
6
7
8
9
10
11
content = 'szzyfimhyzd'
plan = '17,-8'#a和b的值
a = int(plan.split(',')[0])
b = int(plan.split(',')[1])
flag=''
for i in content:
    for j in range(0, 26):
        if (a * j + b) % 26 == ord(i) - ord('a'):
            flag+=chr(97 + j)
print(flag)
#affineshift

猪圈密码

猪圈密码（Pigpen cipher)也称作共济会密码（masonic ciphe）、共济会员密码（Freemason’s cipher）等，是一种以格子为基础的简单替代式密码，把英文字母替换成了各种图形符号。

这是一种外形古怪的密码，已经传递了几百年。早在1700年代，共济会常常使用这种密码保护一些私密纪录或用来通讯。没有人明确知道它是什么时候发明的，但这个密码被一个叫“自由石匠”的组织所使用，也被美国内战时的盟军所使用。

猪圈密码作为一种简单替代式密码，其实可以设计出无数种变种，但此密码易破解。

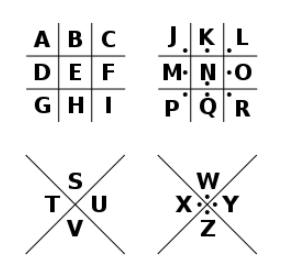
由线和点组成的形状即代表在该形状内的那个字符，比如∧=V、∨=S、⊔=B、⊓=H得到密码表

如明文为 X marks the spot ，那么密文如下

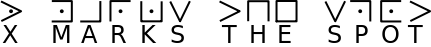
  • 猪圈密码变体0

将上述的密码表做转换：A→J，E→N，I→R

  • 猪圈密码变体1

上述变体的猪圈密码表对应为：

  • 猪圈密码变体2

解密可以使用在线工具：https://www.xiao84.com/tools/103177.html

跳舞的小人

这种密码出自于福尔摩斯探案集。每一个跳舞的小人实际上对应的是英文二十六个字母中的一个，而小人手中的旗子则表明该字母是单词的最后一个字母，如果仅仅是一个单词而不是句子，或者是句子中最后的一个单词，则单词中最后一个字母不必举旗。

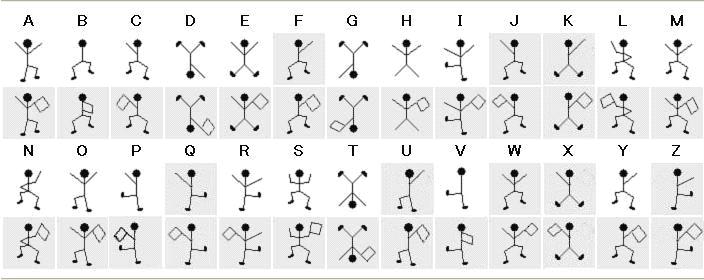
多表替换密码

针对单表代替密码容易被频率分析法破解的缺点，人们提出多表代换密码，用一系列（两个以上）代换表依次对明文消息的字母进行代换。

在多表替换加密中，多表替换的加密过程中由到多张表组成，每个字符分别用不同的密码表进行替换。

多表替换替换密码主要优点就是解决了单表替换密码中频率分析的问题。并且密文跟明文并不是一一对应的

比如：凯撒密码可以变成一种基于密钥的凯撒密码（Keyed Caesar）：利用一个密钥，将密钥的每一位转换为数字（一般转化为字母表对应顺序的数字），分别以这一数字为密钥加密明文的每一位字母。比如：

明文信息：s0a6u3u1s0bv1a

密钥：guangtou

偏移：6，20，0，13，6，19，14，20

密文：y0u6u3h1y0uj1u

http://rumkin.com/tools/cipher/caesar-keyed.php

Vigenere 维吉尼亚密码

维吉尼亚是多表替换密码中比较典型的代表，维吉尼亚密码是在凯撒密码基础上产生的一种加密方法，它将凯撒密码的全部25种位移排序为一张表，与原字母序列共同组成26行及26列的字母表。另外，维吉尼亚密码必须有一个密钥，这个密钥由字母组成，最少一个，最多可与明文字母数量相等。

现有明文：vigenere和密钥：abc

首先，密钥长度需要与明文长度相同，如果少于明文长度，则重复拼接直到相同。本例中，明文长度为3个字母（非字母均被忽略），密钥会被程序补全为”abcabcab”。现在根据如下维吉尼亚密码表格进行加密：

明文第一个字母是v，密钥第一个字母是a，在表格中找到v列与a行相交点，字母v就是密文第一个字母；同理，i列与b行交点字母是j……

密文：vjieogrf

  • 维吉尼亚密码只对字母进行加密，不区分大小写，若文本中出现非字母字符会原样保留。
  • 如果输入多行文本，每行是单独加密的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 维吉尼亚密码解密
content = 'Vjieogrf'
key = 'abc'
flag = ''
num = (len(content) // len(key)) + 1
new_key = key * num  # 拓展key的长度
key_to_num = [ord(k) - 97 for k in new_key]  # 列表推导式，将密钥中的数值转成0到26的值
for i in range(len(content)):
    if content[i].islower():  # 小写字母
        flag += chr((ord(content[i])-97-key_to_num[i])%26+97)  # 加密往前移动，解密往后移动
    elif content[i].isupper(): # 大写字母
        flag += chr((ord(content[i]) - 65 - key_to_num[i]) % 26 + 65)  # 加密往前移动，解密往后移动
    else:
        flag += content[i]
print(flag)

上述代码存在的问题：

  • key_to_num做减法的时候是97，需要考虑到key可能是大写
  • 拓展长度的时候需要计算感觉不太灵活
1
2
3
4
5
6
7
8
9
10
11
12
13
# 维吉尼亚密码解密
content = 'Vjieogrf'
key = 'Abc'
flag = ''
key_to_num = [ord(k) - 97 for k in key.lower()]  # 列表推导式，将密钥中的数值转成0到26的值
for i in range(len(content)):
    if content[i].islower():  # 小写字母
        flag += chr((ord(content[i]) - 97 - key_to_num[i%len(key)]) % 26 + 97)  # 加密往前移动，解密往后移动
    elif content[i].isupper():  # 大写字母
        flag += chr((ord(content[i]) - 65 - key_to_num[i%len(key)]) % 26 + 65)  # 加密往前移动，解密往后移动
    else:
        flag += content[i]
print(flag)

AutokeyCipher

自动密钥密码（Autokey Cipher）也是多表替换密码，与维吉尼亚密码类似，但使用不同的方法生成密钥。通常来说它要比维吉尼亚密码更安全。自动密钥密码主要有两种，关键词自动密钥密码和原文自动密钥密码。下面我们以关键词自动密钥为例：

1
2
3
明文：THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
关键词：CULTURE
根据关键词生成密钥：CULTURE THE QUICK BROWN FOX JUMPS OVER THE

明文的长度跟密钥的长度去掉空格后一样长，然后生成一个跟维吉尼亚密码相似的表格然后得到

1
VBP JOZGD IVEQV HYY AIICX CSNL FWW ZVDP WVK

费纳姆密码

费纳姆密码其实是一种由二进制产生的替换密码，加密时要将明文和密钥都转成7位二进制数。是双方约定一个数，明文异或加上这个数就是密文。这个数相当于密钥（可以是单词 词组 句子 几个字母也行）。

大写字母 ASCⅡ码 大写字母 ASCⅡ码 小写字母 ASCⅡ码 小写字母 ASCⅡ码
A 1000001 N 1001110 a 1100001 n 1101110
B 1000010 O 1001111 b 1100010 o 1101111
C 1000011 P 1010000 c 1100011 p 1110000
D 1000100 Q 1010001 d 1100100 q 1110001
E 1000101 R 1010010 e 1100101 r 1110010
F 1000110 S 1010011 f 1100110 s 1110011
G 1000111 T 1010100 g 1100111 t 1110100
H 1001000 U 1010101 h 1101000 u 1110101
I 1001001 V 1010110 i 1101001 v 1110110
J 1001010 W 1010111 j 1101010 w 1110111
K 1001011 X 1011000 k 1101011 x 1111000
L 1001100 Y 1011001 l 1101100 y 1111001
M 1001101 Z 1011010 m 1101101 z 1111010

原本的ASCII是八位，去掉了第一位的0所以变成了现在这样子

  • 明文： HELLO= 1001000 1000101 1001100 1001100 1001111
  • 密钥：CRUDE= 1000011 1010010 1010101 1000100 1000101
  • 异或后的密文 = 0001011 0010111 0011001 0001000 0001010（得到这个不用再转成ASCII）

异或（xor，python符号（^））：不同为1，相同为0，比如0异或1结果为1，0异或0结果为0。两次异或可以还原成原来的样子

利用上面的异或性质，可以使用密文跟密钥再次异或得到明文的二进制，然后转换成ASCII得到明文，

1
2
3
4
5
6
content='00010110010111001100100010000001010'
key='CRUDE'
mi =[content[i:i+7] for i in range(0,len(content),7)]
flag=''
for i,j in zip(mi,key):#在python中不仅二进制可以做异或，十进制也可以
    print(chr(int(i,2)^ord(j)))

杰斐逊轮转加密

用一组相互独立的转轮，其上是以随机顺序写的26个字母表，这些轮可自由转动，使明文出现在一条直线上 ，而密文可以从其他任意直线选取。

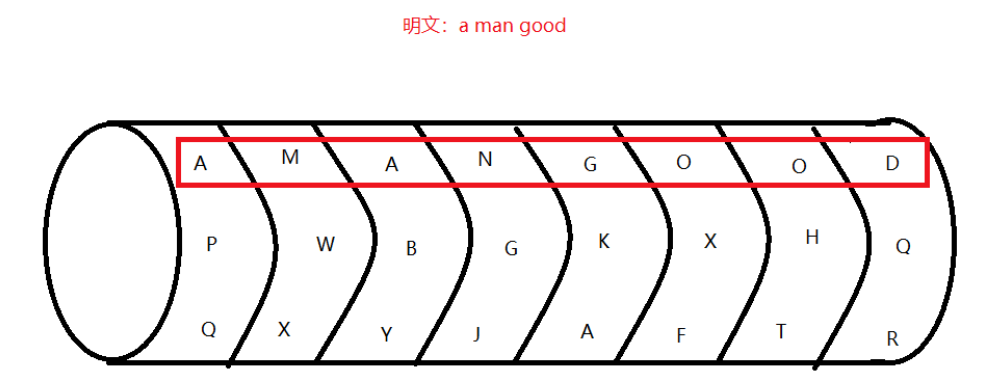
杰斐逊轮转加密每个转轮相当于一个替换字母表，破解难度大，缺点就是传输信息有限，传输的信息不能超过转轮数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
一道题目：墙上写了好多奇奇怪怪的 英文字母，排列的的整整齐齐，店面前面还有一个大大的类似于土耳其旋转烤肉的架子，上面一圈圈的 也刻着很多英文字母，你是一个小历史迷，对于二战时候的历史刚好特别熟悉，一拍大腿：“嗨呀！我知道 是什么东西了！”。提示：托马斯·杰斐逊。 flag，是字符串，小写。
1:   < ZWAXJGDLUBVIQHKYPNTCRMOSFE <
2:   < KPBELNACZDTRXMJQOYHGVSFUWI <
3:   < BDMAIZVRNSJUWFHTEQGYXPLOCK <
4:   < RPLNDVHGFCUKTEBSXQYIZMJWAO <
5:   < IHFRLABEUOTSGJVDKCPMNZQWXY <
6:   < AMKGHIWPNYCJBFZDRUSLOQXVET <
7:   < GWTHSPYBXIZULVKMRAFDCEONJQ <
8:   < NOZUTWDCVRJLXKISEFAPMYGHBQ <
9:   < XPLTDSRFHENYVUBMCQWAOIKZGJ <
10:  < UDNAJFBOWTGVRSCZQKELMXYIHP <
11： < MNBVCXZQWERTPOIUYALSKDJFHG <
12： < LVNCMXZPQOWEIURYTASBKJDFHG <
13： < JZQAWSXCDERFVBGTYHNUMKILOP <
密钥为：2,3,7,5,13,12,9,1,8,10,4,11,6
密文为：NFQKSEVOQOFNP

代码实现解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 杰斐逊轮转加密
value = '''1:< ZWAXJGDLUBVIQHKYPNTCRMOSFE <
2:< KPBELNACZDTRXMJQOYHGVSFUWI <
3: < BDMAIZVRNSJUWFHTEQGYXPLOCK <
4: < RPLNDVHGFCUKTEBSXQYIZMJWAO <
5:   < IHFRLABEUOTSGJVDKCPMNZQWXY <
6:   < AMKGHIWPNYCJBFZDRUSLOQXVET <
7:   < GWTHSPYBXIZULVKMRAFDCEONJQ <
8:   < NOZUTWDCVRJLXKISEFAPMYGHBQ <
9:   < XPLTDSRFHENYVUBMCQWAOIKZGJ <
10:  < UDNAJFBOWTGVRSCZQKELMXYIHP <
11： < MNBVCXZQWERTPOIUYALSKDJFHG <
12： < LVNCMXZPQOWEIURYTASBKJDFHG <
13： < JZQAWSXCDERFVBGTYHNUMKILOP <'''
new = []
for i in value.split('\n'):  # 根据换行来切片
    new.append(i[i.index('<') + 2:i.rindex('<') - 1])  # 处理多余字符
key = [int(i) for i in '2,3,7,5,13,12,9,1,8,10,4,11,6'.split(',')]  # 转成整数
content = 'NFQKSEVOQOFNP'  # 密文
text = []
# for i in range(len(content)):
#     print(content[i:]+content[:i])
for k, m in zip(key, content):
    # print(new[k - 1][new[k - 1].index(m):]+new[k - 1][:new[k - 1].index(m)])
    text.append(new[k - 1][new[k - 1].index(m):]+new[k - 1][:new[k - 1].index(m)])
# print(text)

flag=[]
for i in range(26):#每个列取值
    txt=''
    for j in text:
        txt+=j[i]
    flag.append(txt)
print(flag)
#17列，都是大写FIREINTHEHOLE

Playfair

Playfair 密码（Playfair cipher or Playfair square）是一种替换密码，1854 年由英国人查尔斯 · 惠斯通（Charles Wheatstone）发明，基本算法如下：

  1. 选取一串英文字母，除去重复出现的字母，将剩下的字母逐个逐个加入 5 × 5 的矩阵内，剩下的空间由未加入的英文字母依 a-z 的顺序加入。注意，将 q 去除，或将 i 和 j 视作同一字。
  2. 将要加密的明文分成两个一组。若组内的字母相同，将 X（或 Q）加到该组的第一个字母后，重新分组。若剩下一个字，也加入 X 。
  3. 在每组中，找出两个字母在矩阵中的地方。
    • 若两个字母不同行也不同列，在矩阵中找出另外两个字母（第一个字母对应行优先），使这四个字母成为一个长方形的四个角。
    • 若两个字母同行，取这两个字母右方的字母（若字母在最右方则取最左方的字母）。
    • 若两个字母同列，取这两个字母下方的字母（若字母在最下方则取最上方的字母）。

新找到的两个字母就是原本的两个字母加密的结果。

以 playfair example 为密匙，得5 × 5的矩阵，需要去掉重复的，并且在最后面将没有在里面的补充进去

1
2
3
4
5
P L A Y F
I R E X M
B C D G H
K N O Q S
T U V W Z

要加密的讯息为 Hide the gold in the tree stump，将密文分成两个一组，如果组内字母一样第二位用X代替，如果最后一个只有一个也加入一个X，此处的tree结果就是TR EX

1
HI DE TH EG OL DI NT HE TR EX ES TU MP

然后根据上面的矩阵和规则挨个寻找对应的字母组合，比如：

1
2
3
4
情况一：				   情况二：							情况三：
I R E X M	HI是明文		I R E X M		DE是明文		I R E X M		EX是明文
B C D G H	BM是密文		B C D G H		OD是密文						XM是密文
						  K N O Q S
1
BM OD ZB XD NA BE KU DM UI XM MO UV IF

Polybius

Polybius （波利比奥斯）密码又称为棋盘密码，将给定的明文加密为两两组合的数字，密码表如下

x

明文：HELLO，使用这个表格加密

密文：23 15 31 31 34

hint：i和j需要结合上下文取值

因为Polybius比较简单于是在这个基础上衍生了多种密码表，并且能够定制密码表比如A D F G X

ADFGX密码

1918 年，第一次世界大战将要结束时，法军截获了一份德军电报，电文中的所有单词都由 A、D、F、G、X 五个字母拼成，因此被称为 ADFGX 密码。ADFGX 密码是 1918 年 3 月由德军上校 Fritz Nebel 发明的，是结合了 Polybius 密码和置换密码的双重加密方案。

x

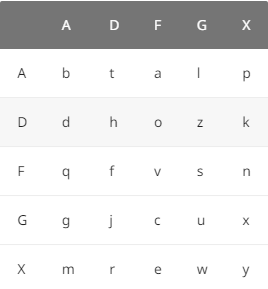
明文：HELLO，使用这个表格加密

密文：DD XF AG AG DF

hint：可以看到这两种密码的密文都是只有五种可能所以可以根据密文类型联想到上面两种密码，并且长度是二的倍数

  • 题目

现有密文：ilnllliiikkninlekile

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
cipher = "ilnllliiikkninlekile"
key = []
for i in itertools.permutations('ilnke', 5):
    key.append(''.join(i))
for now_key in key:
    solve_c = ""
    res = ""
    for now_c in cipher:
        solve_c += str(now_key.index(now_c))
    for i in range(0,len(solve_c),2):
        now_ascii = int(solve_c[i])*5+int(solve_c[i+1])+97
        if now_ascii>ord('i'):
            now_ascii+=1
        res += chr(now_ascii)
    if "flag" in res:
        print (now_key,res)

Nihilist 密码

Nihilist 密码又称关键字密码：明文 + 关键字 = 密文。以关键字 helloworld 为例。

首先利用密钥构造棋盘矩阵（类似 Polybius 密码），新建一个 5 × 5 矩阵，将字符不重复地依次填入矩阵，剩下部分按字母顺序填入，字母 i 和 j 等价

x

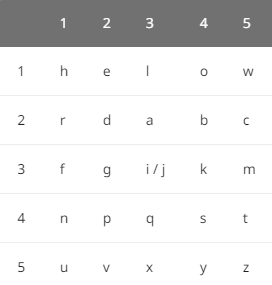
对于加密过程参照矩阵 M 进行加密：

1
2
a -> M[2,3] -> 23
t -> M[4,5] -> 45

对于解密过程

参照矩阵 M 进行解密：

1
2
23 -> M[2,3] -> a
45 -> M[4,5] -> t

hint：密文都是数字并且长度是偶数，而只包含 1 到 5

希尔密码

希尔密码（Hill）使用每个字母在字母表中的顺序作为其对应的数字，即 A=0，B=1，C=2 等，然后将明文转化为 n 维向量，跟一个 n × n 的矩阵相乘，再将得出的结果模 26。注意用作加密的矩阵（即密匙）必须是可逆的，否则就不可能解码。只有矩阵的行列式和 26 互质，才是可逆的。

明文：ACT，转化为矩阵

1
2
3
0
2
19

现有密钥矩阵：

1
2
3
6	24	1
13	16	10
20	17	15

然后解密过程可以表示为

1
2
3
[6	24	1 ]	[0]			[6*0+24*2+1*19]		[67]		[15]
[13	16	10]	[2]		= 	[13*0+16*2+10*19]=	[222]mod 26=[14]
[20	17	15]	[19]		[20*0+17*2+15*19]	[319]		[7]

所以得到密文为：POH

  • 题目

密文： 22,09,00,12,03,01,10,03,04,08,01,17 （wjamdbkdeibr）

使用的矩阵是 1 2 3 4 5 6 7 8 10

首先，矩阵是 3 × 3 的。说明每次加密 3 个字符。

这个矩阵是按照列来排布的。即如下

1
2
3
1 4 7
2 5 8
3 6 10

最后的结果为 overthehillx

其他类型的加密

当铺密码

当铺密码就是一种将中文和数字进行转化的密码，算法相当简单:当前汉字有多少笔画出头，就是转化成数字几

当铺密码是一种将汉字和数字进行转化的密码

算法相当简单，当前汉字有多少笔画出头，就是转化为数字几

例如羊这个字，出头的地方有九个，所以转化为9

那么”羊由大井夫大人王中工”可以转为以下数字：

9158753624

云影加密

该密码又称为01248 密码 ，使用 0，1，2，4，8 四个数字，其中 0 用来表示间隔，其他数字以加法可以表示出 如：28=10，124=7，18=9，再用 1->26 表示 A->Z。

hint：云影加密只有 0，1，2，4，8

  • 题目

8842101220480224404014224202480122，根据0来切割得到

切片结果 运算 运算结果 结果对应的字符
88421 8+8+4+2+1 23 W
122 1+2+2 5 E
48 4+8 12 L
2244 2+2+4+4 12 L
4 4 4 D
142242 1+4+2+2+4+2 15 O
248 2+4+8 14 N
122 1+2+2 5 E

所以解密结果为：WELLDONE

python代码实现

1
2
3
4
5
6
7
8
9
10
content='8842101220480224404014224202480122'
charList = [chr(i) for i in range(ord('A'), ord('Z') + 1)]
ret = []
plaintext = [i for i in content.split('0')]
for i in plaintext:
    tmp = 0
    for j in range(len(i)):
        tmp += int(i[j])
    ret.append(charList[tmp - 1])
print('云影密码', ''.join(ret))

base家族解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
##base家族解密
import base64
import base128
import base36
import base58
import base91
import py3base92

content = 密文信息
num=[]
while True:
    try:
        content = base64.b16decode(content).decode()
        num.append('base16')
        continue
    except:
        pass
    try:
        content = base64.b32decode(content).decode()
        num.append('base32')
        continue
    except:
        pass
    try:
        content = base36.dumps(content).decode()
        num.append('base36')
        continue
    except:
        pass
    try:
        content = base58.b58decode(content).decode()
        num.append('base58')
        continue
    except:
        pass
    try:
        content = base64.b64decode(content).decode()
        num.append('base64')
        continue
    except:
        pass
    try:
        content = base64.b85decode(content).decode()
        num.append('base85')
        continue
    except:
        pass
    try:
        content = base64.a85decode(content).decode()
        num.append('base85')
        continue
    except:
        pass
    try:
        content = base91.decode(content).decode()
        num.append('base91')
        continue
    except:
        pass
    try:
        content = py3base92.b92decode(content).decode()
        num.append('base92')
        continue
    except:
        pass
    try:
        content = b''.join(base128.base128(chars = None, chunksize = 7) .decode(content)).decode()
        num.append('base128')
        continue
    except:
        pass
    break
print(num)
print(content)

pycipher库的使用

pycipher是python的一个函数库，使用pip install pycipher即可安装

1
2
3
>>> import pycipher
>>> dir(pycipher)
['ADFGVX', 'ADFGX', 'Affine', 'Atbash', 'Autokey', 'Beaufort', 'Bifid', 'Caesar', 'ColTrans', 'Enigma', 'Foursquare', 'FracMorse', 'Gronsfeld', 'M209', 'Playfair', 'PolybiusSquare', 'Porta', 'Railfence', 'Rot13', 'SimpleSubstitution', 'Vigenere', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', '__version__', 'adfgvx', 'adfgx', 'affine', 'atbash', 'autokey', 'base', 'beaufort', 'bifid', 'caesar', 'columnartransposition', 'enigma', 'foursquare', 'fracmorse', 'gronsfeld', 'm209', 'playfair', 'polybius', 'porta', 'pycipher', 'railfence', 'rot13', 'simplesubstitution', 'util', 'vigenere']

使用dir(pycipher)可以查询包括的类，能够实现多种古典密码的加解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
>>> help(pycipher.Caesar)
Help on class Caesar in module pycipher.caesar:
class Caesar(pycipher.base.Cipher)
 |  Caesar(key=13)
 |  The Caesar Cipher has a key consisting of an integer 1-25.
 |  This cipher encrypts a letter according to the following equation::
 |
 |      c = (p + key)%26
 |
 |  where c is the ciphertext letter, p the plaintext letter.
 |  For more details on the Caesar cipher, see http://www.practicalcryptography.com/ciphers/caesar-cipher/
 |  :param key: The additive key. Allowable values are integers 0-25.
 |
 |  Method resolution order:
 |      Caesar
 |      pycipher.base.Cipher
 |      builtins.object
 |  Methods defined here:
 |  __init__(self, key=13)
 |      Initialize self.  See help(type(self)) for accurate signature.
 |
 |  decipher(self, string, keep_punct=False)
 |      Decipher string using Caesar cipher according to initialised key.
 |      Example::
 |
 |          plaintext = Caesar(3).decipher(ciphertext)
 |
 |      :param string: The string to decipher.
 |      :param keep_punct: if true, punctuation and spacing are retained. If false, it is all removed. Default is False.
 |      :returns: The deciphered string.
 |
 |  encipher(self, string, keep_punct=False)
 |      Encipher string using Caesar cipher according to initialised key.
 |      Example::
 |
 |          ciphertext = Caesar(3).encipher(plaintext)
 |
 |      :param string: The string to encipher.
 |      :param keep_punct: if true, punctuation and spacing are retained. If false, it is all removed. Default is False.
 |      :returns: The enciphered string.

可以使用help(pycipher.Caesar)对一个类里面包含的函数信息

栅栏密码快速实现

1
2
3
>>> import pycipher
>>> pycipher.Caesar(3).decipher("IODJ{Khuh_lv_brxu_iodj}")
'FLAGHEREISYOURFLAG'

可以看到encipher加密和decipher解密，但是需要指定密钥，然后输出有只有大写，可以修改

Atbash Cipher密码脚本可以快速实现

1
2
3
4
5
>>>from pycipher import Atbash
>>>Atbash().encipher('defend the east wall of the castle')
'wvuvmwgsvvzhgdzoolugsvxzhgov'
>>>Atbash().decipher('wvuvmwgsvvzhgdzoolugsvxzhgov')
'defendtheeastwallofthecastle'

仿射密码快速实现

1
2
3
4
5
>>> import pycipher
>>> pycipher.Affine(11,7).decipher('dikxourxd')
'CTFSDNISC'
>>> pycipher.Affine(17,-8).decipher('szzyfimhyzd')
'AFFINESHIFT'

Vigenere 维吉尼亚密码快速实现

1
2
3
>>> import pycipher
>>> pycipher.Vigenere("abc").decipher('Vjieogrf')
'VIGENERE'

列置换快速实现

1
2
3
4
5
>>> import pycipher
>>> pycipher.ColTrans('nice').encipher('ilovepythonandctf')
'OYNCVTATLPODIEHNF'
>>> pycipher.ColTrans('nice').decipher('OYNCVTATLPODIEHNF')
'ILOVEPYTHONANDCTF'

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
# 栅栏加解密
# crypto='flag{012345}'
# for i in range(0,6):
#     for n in range(i,len(crypto),6):
#         print(crypto[n],end='')
# print()
# zhalan='f1l2a3g4{50}'
# for i in range(0,2):
#     for n in range(i,len(zhalan),2):
#         print(zhalan[n], end='')


# # 栅栏加解密合并
# def railfence(content):
#     all=[]
#     for key in range(2,len(content)):
#         flag=''
#         if len(content)%key==0:
#             for i in range(0, key):
#                 for n in range(i, len(content), key):
#                     flag=flag+content[n]
#                     # print(content[n], end='')
#             all.append('栏数为:{0}时,结果为:{1}'.format(key,flag))
#     print(all)
#     print(len(all))
# if __name__ == '__main__':
#     content='flag{012345}'
#     railfence(content)
#     content='f{3l04a15g2}'
#     railfence(content)


# #莫斯密码加解密
# def mosdecrypt(content):
#     MorseList = {'A': ".-", 'B': "-...", 'C': "-.-.", 'D': "-..", 'E': ".", 'F': "..-.", 'G': "--.",
#                  'H': "....", 'I': "..", 'J': ".---", 'K': "-.-", 'L': ".-..", 'M': "--", 'N': "-.",
#                  'O': "---", 'P': ".--.", 'Q': "--.-", 'R': ".-.", 'S': "...", 'T': "-", 'U': "..-",
#                  'V': "...-", 'W': ".--", 'X': "-..-", 'Y': "-.--", 'Z': "--..",
#                  '1': ".----", '2': "..---", '3': "...--", '4': "....-", '5': ".....",
#                  '6': "-....", '7': "--...", '8': "---..", '9': "----.", '0': "-----",
#                  '.': ".-.-.-", '?': "..--..", '!': "-.-.--", '(': "-.--.", '@': ".--.-.", ':': "---...",
#                  '=': "-...-", '-': "-....-", ')': "-.--.-", ',': "--..--", '\'': ".----.", '_': "..--.-",
#                  '$': "...-..-", ';': "-.-.-.", '/': "-..-.", '\"': ".-..-.", '&': ".-...",
#                  '+': ".-.-.",
#                  'à': ".--.-", 'ä': ".-.-", 'ch': "----", 'ç': "-.-..", 'ð': "..--.",
#                  'é': "..-..", 'è': ".-..-", 'ĝ': "--.-.", 'ĥ': "-.--.", 'ĵ': ".---.",
#                  'ñ': "--.--", 'ø': "---.", 'ŝ': "...-.", 'þ': ".--..", 'ü': "..--",}
#     if '0' in content and '1' in content:
#         trans = ''.maketrans('01', '.-')
#         content = content.translate(trans)
#     if '－' in content or '·' in content:
#         content=content.replace('－','-')
#         content=content.replace('·','.')
#     if '/' in content:
#         lmorsecodeList = content.split("/")
#     else:
#         content = content.replace(' ', '/')
#         if '///' in  content:
#             content = content.replace('///', '/ /')
#         lmorsecodeList = content.split("/")
#     print(lmorsecodeList)
#     flag = ''
#     for char in lmorsecodeList:
#         if char ==' ':
#             flag = flag +  char
#         for k, v in MorseList.items():
#             if v == char:
#                 flag = flag + k
#     print("莫斯密码小写:", flag)
#     print("莫斯密码大写:", flag.lower())
#     return flag
# content='··   ·－·· －－－ ···－ ·   －·－－ －－－ ··－ '
# print(content.split(" "))
# print(mosdecrypt(content))


# # 凯撒密码
# def caesar_Crypto(content):
#     all_plain=[]
#     for num in range(1,26):
#         plain = ''
#         for i in content:
#             if i.islower():#小写字母
#                 plain = plain + chr(97 + (ord(i) + num - 97) % 26)
#             elif i.isupper():#大写字母
#                 plain = plain + chr(65 + (ord(i) + num - 65) % 26)
#             else:#上面两者都不是
#                 plain=plain+i
#         print(plain)
#         all_plain.append(plain)
#     print(all_plain)
# content='IODJ{Khuh_lv_brxu_iodj}'
# caesar_Crypto(content)


# # 凯撒密码新思路
# 实现循环
# crypto='abcdefghijklmnopqrstuvwxyz'
# for i in range(len(crypto)):
#     print(crypto[i:]+crypto[:i])
# def caesar_Crypto(content):
#     all_plain=[]
#     lowercase = 'abcdefghijklmnopqrstuvwxyz'
#     uppercase = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
#     for num in range(1,26):
#         lower=lowercase[num:]+lowercase[:num]
#         upper=uppercase[num:]+uppercase[:num]
#         plain=''
#         table=''.maketrans(lower+upper,lowercase+uppercase)
#         for i in content:
#             plain=plain+i.translate(table)
#         all_plain.append(plain)
#         print(plain)
#     print(all_plain)
# content='IODJ{Khuh_lv_brxu_iodj}'
# caesar_Crypto(content)
# 变异凯撒
# str="afZ_r9VYfScOeO_UL^RWUc"
# a=5
# for i in str:
#     print(chr(ord(i)+a),end='')
#     a=a+1

# ROT5
# def caesar_Crypto(content):
#     all_plain=[]
#     lowercase = '0123456789'
#     lower=lowercase[5:]+lowercase[:5]
#     plain=''
#     table=''.maketrans(lower,lowercase)
#     for i in content:
#         plain=plain+i.translate(table)
#     all_plain.append(plain)
#     print(plain)
# content='flag{5678901}'
# caesar_Crypto(content)


# Atbash Cipher
# def caesar_Crypto(content):
#     all_plain=[]
#     lowercase = 'abcdefghijklmnopqrstuvwxyz'
#     lower=lowercase[::-1]#此处需要修改
#     plain=''
#     table=''.maketrans(lower,lowercase)
#     for i in content:
#         plain=plain+i.translate(table)
#     all_plain.append(plain)
#     print(plain)
# content='the quick brown fox jumps over the lazy dog'
# caesar_Crypto(content)
# content='gsv jfrxp yildm ulc qfnkh levi gsv ozab wlt'
# caesar_Crypto(content)
# #flag{0123456}


# 培根密码大小写提取
# a='SjkLnIljKHamJmkilABawiiioaAMbOaPIJmklNBaKijmBuaoljiAUWMakMHWNAakm'
# flag=''
# for i in a:
#     if i.islower():
#         flag+='A'
#     elif i.isupper():
#         flag+="B"
# print(flag)
# table=''.maketrans("AB","BA")
# print(flag.translate(table))


# 列表转换成字典
# alphabet = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
# cipher = ["aaaaa","aaaab","aaaba","aaabb","aabaa","aabab","aabba","aabbb","abaaa","abaab","ababa","ababb","abbaa","abbab","abbba","abbbb","baaaa","baaab","baaba","baabb","babaa","babab","babba","babbb","bbaaa","bbaab"]
# print(dict(zip(alphabet,cipher)))
# #{'a': 'aaaaa', 'b': 'aaaab', 'c': 'aaaba', 'd': 'aaabb', 'e': 'aabaa', 'f': 'aabab', 'g': 'aabba', 'h': 'aabbb', 'i': 'abaaa', 'j': 'abaab', 'k': 'ababa', 'l': 'ababb', 'm': 'abbaa', 'n': 'abbab', 'o': 'abbba', 'p': 'abbbb', 'q': 'baaaa', 'r': 'baaab', 's': 'baaba', 't': 'baabb', 'u': 'babaa', 'v': 'babab', 'w': 'babba', 'x': 'babbb', 'y': 'bbaaa', 'z': 'bbaab'}

# 培根密码26长度
# txt = 'SjkLnIljKHamJmkilABawiiioaAMbOaPIJmklNBaKijmBuaoljiAUWMakMHWNAakm'
# content = ''
# for i in txt:
#     if i.islower():
#         content += 'a'
#     elif i.isupper():
#         content += "b"
# if len(content) % 5 == 0:
#     # alphabet = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
#     alphabet = [chr(i) for i in range(ord('a'), ord('z') + 1)]
#     cipher = ["aaaaa", "aaaab", "aaaba", "aaabb", "aabaa", "aabab", "aabba", "aabbb", "abaaa", "abaab", "ababa",
#               "ababb", "abbaa", "abbab", "abbba", "abbbb", "baaaa", "baaab", "baaba", "baabb", "babaa", "babab",
#               "babba", "babbb", "bbaaa", "bbaab"]
#     key = dict(zip(cipher, alphabet))  # 生成键值对应的字典
#     try:
#         flag = ''
#         for i in range(0, len(content), 5):
#             value = content[i:i + 5]  # 切片
#             flag += key.get(value)  # 取键值
#     except:
#         flag = ''
#         table = ''.maketrans("ab", "ba")
#         content = content.translate(table)
#         for i in range(0, len(content), 5):
#             value = content[i:i + 5]  # 切片
#             flag += key.get(value)  # 取键值
#     print(flag)
# else:
#     print("不是培根密码")
#
# 培根密码24长度
# txt = 'SjkLnIljKHamJmkilABawiiioaAMbOaPIJmklNBaKijmBuaoljiAUWMakMHWNAakm'
# content = ''
# for i in txt:
#     if i.islower():
#         content += 'a'
#     elif i.isupper():
#         content += "b"
# content='ABABAABAAABAABBAABAA'.lower()
# if len(content) % 5 == 0:
#     alphabet = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', '(ij)', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't',
#                 '(uv)', 'w', 'x', 'y', 'z']
#     cipher = ["aaaaa", "aaaab", "aaaba", "aaabb", "aabaa", "aabab", "aabba", "aabbb", "abaaa", "abaab",
#               "ababa", "ababb", "abbaa", "abbab", "abbba", "abbbb", "baaaa", "baaab", "baaba", "baabb",
#               "babaa", "babab", "babba", "babbb"]
#     key = dict(zip(cipher, alphabet))  # 生成键值对应的字典
#     try:
#         flag = ''
#         for i in range(0, len(content), 5):
#             value = content[i:i + 5]  # 切片
#             flag += key.get(value)  # 取键值
#     except:
#         flag = ''
#         table = ''.maketrans("ab", "ba")
#         content = content.translate(table)
#         for i in range(0, len(content), 5):
#             value = content[i:i + 5]  # 切片
#             flag += key.get(value)  # 取键值
#     print(flag)
# else:
#     print("不是培根密码")

# 乘法逆元
# m=1
# while True:
#     if (7*m)%26==1:
#         print(m)
#         break
#     m=m+1
# for i in range(0,26):
#     if (7 * i) % 26 == 25:
#         print(i)

# 仿射密码解密
# 加密公式：c=(11m+7)mod26,对应的a=11,b等于7
# content = 'dikxourxd'
# m = 1
# while True:
#     if (11 * m) % 26 == 1:
#         print(m)  # 得到乘法逆元
#         break
#     m = m + 1
# flag=''
# for i in content:
#     flag+=chr(97 + (ord(i) - 97 - 7) * 19 % 26)
#     print(chr(97 + (ord(i) - 97 - 7) * 19 % 26))
# print(flag)
# 暴力破解
# content = 'szzyfimhyzd'
# plan = '17,-8'#a和b的值
# a = int(plan.split(',')[0])
# b = int(plan.split(',')[1])
# flag=''
# for i in content:
#     for j in range(0, 26):
#         if (a * j + b) % 26 == ord(i) - ord('a'):
#             flag+=chr(97 + j)
# print(flag)


# # 维吉尼亚密码解密
# content = 'Vjieogrf'
# key = 'abc'
# flag = ''
# key_to_num = [ord(k) - 97 for k in key.lower()]  # 列表推导式，将密钥中的数值转成0到26的值
# for i in range(len(content)):
#     if content[i].islower():  # 小写字母
#         flag += chr((ord(content[i]) - 97 - key_to_num[i%len(key)]) % 26 + 97)  # 加密往前移动，解密往后移动
#     elif content[i].isupper():  # 大写写字母
#         flag += chr((ord(content[i]) - 65 - key_to_num[i%len(key)]) % 26 + 65)  # 加密往前移动，解密往后移动
#     else:#其他字符保留
#         flag += content[i]
# print(flag)
# # 维吉尼亚密码解密
# import pycipher
# print(pycipher.Vigenere("abc").decipher('Vjieogrf'))


# 费纳姆密码
# content='00010110010111001100100010000001010'
# key='CRUDE'
# mi =[content[i:i+7] for i in range(0,len(content),7)]
# flag=''
# for i,j in zip(mi,key):#在python中不仅二进制可以做异或，十进制也可以
#     print(chr(int(i,2)^ord(j)))

#
# # 杰斐逊轮转加密
# value = '''1:< ZWAXJGDLUBVIQHKYPNTCRMOSFE <
# 2:< KPBELNACZDTRXMJQOYHGVSFUWI <
# 3: < BDMAIZVRNSJUWFHTEQGYXPLOCK <
# 4: < RPLNDVHGFCUKTEBSXQYIZMJWAO <
# 5:   < IHFRLABEUOTSGJVDKCPMNZQWXY <
# 6:   < AMKGHIWPNYCJBFZDRUSLOQXVET <
# 7:   < GWTHSPYBXIZULVKMRAFDCEONJQ <
# 8:   < NOZUTWDCVRJLXKISEFAPMYGHBQ <
# 9:   < XPLTDSRFHENYVUBMCQWAOIKZGJ <
# 10:  < UDNAJFBOWTGVRSCZQKELMXYIHP <
# 11： < MNBVCXZQWERTPOIUYALSKDJFHG <
# 12： < LVNCMXZPQOWEIURYTASBKJDFHG <
# 13： < JZQAWSXCDERFVBGTYHNUMKILOP <'''
# new = []
# for i in value.split('\n'):  # 根据换行来切片
#     new.append(i[i.index('<') + 2:i.rindex('<') - 1])  # 处理多余字符
# key = [int(i) for i in '2,3,7,5,13,12,9,1,8,10,4,11,6'.split(',')]  # 转成整数
# content = 'NFQKSEVOQOFNP'  # 密文
# text = []
# # for i in range(len(content)):
# #     print(content[i:]+content[:i])
# for k, m in zip(key, content):
#     # print(new[k - 1][new[k - 1].index(m):]+new[k - 1][:new[k - 1].index(m)])
#     text.append(new[k - 1][new[k - 1].index(m):]+new[k - 1][:new[k - 1].index(m)])
# # print(text)
#
# flag=[]
# for i in range(26):
#     txt=''
#     for j in text:
#         txt+=j[i]
#     flag.append(txt)
# print(flag)
# #17列



# #base家族解密
# import base64
# import base128
# import base36
# import base58
# import base91
# import py3base92
#
# content = '='
# num=[]
# while True:
#     try:
#         content = base64.b16decode(content).decode()
#         num.append('base16')
#         continue
#     except:
#         pass
#     try:
#         content = base64.b32decode(content).decode()
#         num.append('base32')
#         continue
#     except:
#         pass
#     try:
#         content = base36.dumps(content).decode()
#         num.append('base36')
#         continue
#     except:
#         pass
#     try:
#         content = base58.b58decode(content).decode()
#         num.append('base58')
#         continue
#     except:
#         pass
#     try:
#         content = base64.b64decode(content).decode()
#         num.append('base64')
#         continue
#     except:
#         pass
#     try:
#         content = base64.b85decode(content).decode()
#         num.append('base85')
#         continue
#     except:
#         pass
#     try:
#         content = base64.a85decode(content).decode()
#         num.append('base85')
#         continue
#     except:
#         pass
#     try:
#         content = base91.decode(content).decode()
#         num.append('base91')
#         continue
#     except:
#         pass
#     try:
#         content = py3base92.b92decode(content).decode()
#         num.append('base92')
#         continue
#     except:
#         pass
#     try:
#         content = b''.join(base128.base128(chars = None, chunksize = 7) .decode(content)).decode()
#         num.append('base128')
#         continue
#     except:
#         pass
#     break
# print(num)
# print(content)




##ADFGX密码
# import itertools
# cipher = "ilnllliiikkninlekile"
# key = []
# for i in itertools.permutations('ilnke', 5):
#     key.append(''.join(i))
# for now_key in key:
#     solve_c = ""
#     res = ""
#     for now_c in cipher:
#         solve_c += str(now_key.index(now_c))
#     for i in range(0,len(solve_c),2):
#         now_ascii = int(solve_c[i])*5+int(solve_c[i+1])+97
#         if now_ascii>ord('i'):
#             now_ascii+=1
#         res += chr(now_ascii)
#     if "flag" in res:
#         print (now_key,res)



### 云影加密
# content='8842101220480224404014224202480122'
# charList = [chr(i) for i in range(ord('A'), ord('Z') + 1)]
# ret = []
# plaintext = [i for i in content.split('0')]
# for i in plaintext:
#     tmp = 0
#     for j in range(len(i)):
#         tmp += int(i[j])
#     ret.append(charList[tmp - 1])
# print('云影密码', ''.join(ret))

参考链接

https://www.oscca.gov.cn/sca/zxfw/2017-04/24/content_1011709.shtml